Norton's Theorem

Norton's Theorem states that it is possible to simplify any linear circuit, no matter how complex, to an equivalent circuit with just a single current source and parallel resistance connected to a load. Just as with Thevenin's Theorem, the qualification of “linear” is identical to that found in the Superposition Theorem: all underlying equations must be linear (no exponents or roots).

 

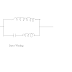
From the previous topic above, it was learned that a somewhat modified approach of Thevenin was formulated. This modified approach is to convert the original network into a simple circuit in which a parallel combination of constant-current source and looking-back resistance "feeds" the load resistor. Take a look on the figure below

 

Take note that Norton's theory also make use of the resistance looking back into the network from the load resistance terminals, with all potential sources replaced by the zero-resistance conductors. It also employs a fictitious source which delivers a constant current, which is equal to the current that would pass into a short circuit connected across the output terminals of the original circuit. 

From the fig (b) above of Norton's equivalent circuit, the load current would be

I_L = I_N R_N / R_N+R_L ---------------2