Maximum Power Transfer Theorem

The Maximum Power Transfer Theorem is not so much a means of analysis as it is an aid to system design. Simply stated, the maximum amount of power will be dissipated by a load resistance when that load resistance is  equal to the Thevenin/Norton  resistance  of  the network   supplying   the  power. If  the  load  resistance  is  lower  or  higher  than  the Thevenin/Norton resistance of the source network, its dissipated power will  be less than maximum.

                     

Taking our Thevenin equivalent example circuit, the Maximum Power Transfer Theorem tells us that the load resistance resulting in greatest power dissipation is equal in value to the Thevenin resistance

This is essentially what is aimed for in radio transmitter design , where  the  antenna or transmission line “impedance” is  matched  to  final power amplifier    “impedance” for maximum radio frequency power output.  Impedance,  the overall opposition to AC and DC current, is very similar to resistance, and must be equal between source and load for the greatest amount of power to be transferred to the load. A load impedance that is too high will result in low power output. A load impedance that is too low will not only result in low power output, but possibly overheating of the amplifier due to the power dissipated in its internal (Thevenin or Norton) impedance.

The Maximum Power Transfer Theorem is not: Maximum power transfer does not coincide with maximum efficiency. Application of The Maximum Power Transfer theorem to AC power distribution will not result in maximum or even high efficiency. The goal of high efficiency is more important for AC power distribution, which dictates a relatively low generator impedance compared to load impedance.

Read More

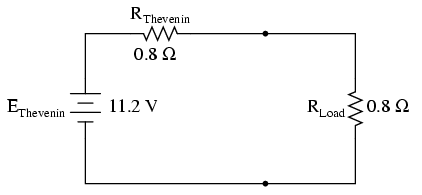
Thevenin's Theorem

Since Thevenin's and Norton's Theorems are two equally valid methods of reducing a complex network down to something simpler to analyze,Consider the figure below which schematically represents the two-terminal network of constant emf's and resistances; a high-resistance voltmeter, connected to the accessible terminals, will indicate the so called open circuit voltage voc. If an extremely low-resistance ammeter is next connected to the same terminals, as in fig.(b), which is so called the short-circuit current iscwill be measured.

Test circuits for Thevenin's Theorem

Now the two quantities determined above may be used to represent an equivalent simple network consisting of the single resistance RTH, which is equal to voc/isc. If the resistor RL is connected to the two terminals, the load current of the circuit will be

                                                  IL = voc / RTH+RL---------------1

The analysis leading to the equation no.1 above was first proposed by M.L. Thevenin the latter part of the nineteenth century, and has been recognized as an important principle in electric circuit theory. His theory was stated as follows: In any two-terminal network of fixed resistances and constant sources of emf, the current in the load resistor connected to the output terminals is equal to the current that would exist in the same resistor if it were connected in series with (a) a simple emf whose voltage is measured at the open-circuited network terminals and (b) a simple resistance whose magnitude is that of the network looking back from the two terminals into the network with all sources of emf replaced by their internal resistances.

Thevenin's Theorem has been applied to many network solutions which considerably simplify the calculations as well as reduce the number of computations.

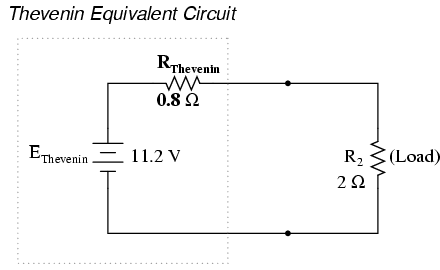                                                                              Thevenine Equivalent Circuit

Read More

Superposition Theorem

Superposition theorem is one of those strokes of genius that takes a complex subject and simplifies it in a way that makes perfect sense. A theorem like Millman's certainly works well, but it is not quite obvious why it works so well. Superposition, on the other hand, is obvious.

The strategy used in the Superposition Theorem is to eliminate all but one source of power within a network at a time, using series/parallel analysis to determine voltage drops (and/or currents) within the modified network for each power source separately. Then, once voltage drops and/or currents have been determined for each power source working separately, the values are all “superimposed” on top of each other (added algebraically) to find the actual voltage drops/currents with all sources active. Let's look at our example circuit again and apply Superposition Theorem to it:

Since we have two sources of power in this circuit, we will have to calculate two sets of values for voltage drops and/or currents, one for the circuit with only the 28 volt battery in effect. . .

            

                 . . and one for the circuit with only the 7 volt battery in effect:
              

                         

 The theorem states like this: In the network of resistors that is energized by two or more sources of emf, (a) the current in any resistor or (b) the voltage across any resistor is equal to: (a) the algebraic sum of the separate currents in the resistor or (b) the voltages across the resistor, assuming that each source of emf, acting independently of the others, is applied separately in turn while the others are replaced by their respective internal values of resistance.

This theorem is illustrated in the given circuit below:

                      

 The original circuit above ( left part ) have one emf source and a current source. If you like to obtain the current I which is equal to the sum of I' + I"using the superposition theorem, we need to do the following steps:

a. Replace the current source I_o by an open circuit. Therefore, an emf source v_o will act independently having a current I' as the first value obtained when the circuit computed.

b. Replace emf source v_o by a short circuit. This time I_o will act independently and I" now will be obtained when the circuit computed.

c. The two values obtained ( I' and I") with emf and current source acting independently will be added to get I = I' + I"

Read More

Norton's Theorem

Norton's Theorem states that it is possible to simplify any linear circuit, no matter how complex, to an equivalent circuit with just a single current source and parallel resistance connected to a load. Just as with Thevenin's Theorem, the qualification of “linear” is identical to that found in the Superposition Theorem: all underlying equations must be linear (no exponents or roots).

 

From the previous topic above, it was learned that a somewhat modified approach of Thevenin was formulated. This modified approach is to convert the original network into a simple circuit in which a parallel combination of constant-current source and looking-back resistance "feeds" the load resistor. Take a look on the figure below

 

Take note that Norton's theory also make use of the resistance looking back into the network from the load resistance terminals, with all potential sources replaced by the zero-resistance conductors. It also employs a fictitious source which delivers a constant current, which is equal to the current that would pass into a short circuit connected across the output terminals of the original circuit. 

From the fig (b) above of Norton's equivalent circuit, the load current would be

I_L = I_N R_N / R_N+R_L ---------------2

Read More

Network Analysis for electric circuits

Network  Analysis  for  electric circuits  are  the  different  useful  techniques related to several currents, emfs, and resistance voltages  in  such  circuit. This is  somewhat  the collection of techniques of finding the voltages and currents in  every component of the network. Some of those  techniques  are  already  mentioned in  this  online  tutorial  of

Electrical Engineering. 

• Kirchhoff''s Voltage Law or KVL
• Kirchhoff''s Current Law or KCL

There are six remaining useful techniques that we are going to learn. The practical example of each analysis will be given in my next post. This is for you to comprehend first what each theory is all about. So, let's begin the first useful technique in analyzing network.  

Anyone  who's  studied  geometry  should  be  familiar with  the  concept  of a  theorem:  a 

relatively simple rule used to solve a  problem,  derived  from  a  more  intensive  analysis 

using fundamental rules of mathematics.  

At  least  hypothetically, any problem in math can be solved just by using the simple rules  of  arithmetic  (in fact, this is how modern digital computers   carry  out  the  most  complex  mathematical  calculations: by repeating many cycles of  additions  and subtractions!), but human beings aren't as consistent or as fast as a digital computer. We need “shortcut” methods  in order  to  avoid  procedural  errors.

In electric network analysis, the fundamental rules are Ohm's Law  and Kirchhoff's Laws. While these humble laws may be applied to analyze just about any  circuit configuration (even if we have to resort to complex algebra to handle multiple unknowns), there are some “shortcut” methods of analysis to make the math  easier for the  average human.

As with any theorem of geometry or algebra, these network  theorems  are derived from fundamental rules. In this chapter, I'm not going to delve into the formal proofs of any of these theorems. If you doubt their validity, you can always empirically  test  them  by  setting  up  example  circuits  and calculating values using the “old” (simultaneous equation) methods versus the “new” theorems, to see if the answers coincide. They always should!

Read More